Spatial correlations of dog bite incidents and dog licenses
To assess whether the spatial distribution of dog license issuance and dog bite incidents in New York City exhibits spatial correlations and clustering characteristics, this study calculated both the global and local Moran’s I for these variables during the research period.
Moran’s I is a statistical metric commonly used in spatial data analysis to measure the degree of spatial autocorrelation. It is employed to determine whether there is a trend of spatial clustering or dispersion in spatial data.
Global Moran’s I
The global Moran’s I is used to describe the average degree of association between all spatial elements and their neighboring elements across the entire study area. The formula for calculation is as follows:
\[ I = \frac{n}{{S_0}} \times \frac{\sum\limits_{i = 1}^n \sum\limits_{j = 1}^n w_{ij}(y_i - \bar{y})(y_j - \bar{y})}{\sum\limits_{i = 1}^n (y_i - \bar{y})^2} \]
Where \(n\) represents the total number of spatial elements,\({S_0} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_{ij}}} }\) is the sum of all spatial weights, \(y_i\) and \(y_j\) denote the attribute values of the \(i^{th}\) and \(j^{th}\) spatial elements, respectively, \(\bar y\) is the mean of the attribute values for all spatial elements, \({w_{ij}}\) is the spatial weight between elements \(i\) and \(j\), and \(I\) is the global Moran’s I, which ranges from \([-1, 1]\). The specific implications of this range are as shown in the following table.
data <- data.frame(
`Range` = c("I > 0", "I < 0", "I = 0"),
`Implication` = c(
"Attribute values of elements exhibit positive spatial autocorrelation, meaning similar attributes cluster together (high values are adjacent to high values, and low values to low values).",
"Attribute values of elements exhibit negative spatial autocorrelation, meaning different attributes cluster together (high values are adjacent to low values, and low values to high values).",
"The attributes are randomly distributed, indicating no spatial autocorrelation."
)
)
kable(data, format = "pipe", align = "c", caption = "Implications of Global Moran's I")| Range | Implication |
|---|---|
| I > 0 | Attribute values of elements exhibit positive spatial autocorrelation, meaning similar attributes cluster together (high values are adjacent to high values, and low values to low values). |
| I < 0 | Attribute values of elements exhibit negative spatial autocorrelation, meaning different attributes cluster together (high values are adjacent to low values, and low values to high values). |
| I = 0 | The attributes are randomly distributed, indicating no spatial autocorrelation. |
To conduct spatio-temporal analysis, it is first necessary to obtain
the adjacency matrix of each zipcode in New York City. The
relativeneigh function in R, part of the spdep
package, is specifically designed to establish adjacency relationships
based on the graphical relationships derived from the distribution of
point features. A key advantage of this function is that it avoids the
intersection of lines connecting neighboring elements, which aligns more
closely with common perceptions of “adjacency.” This function generates
a graph object that can be converted into a neighbor list using
graph2nb. The relative neighborhood graph is defined such
that two points \(x\) and \(y\) are considered neighbors if there is no
other point \(z\) closer to either
\(x\) or \(y\) than they are to each other.
#Relative
shp_point = st_centroid(st_geometry(shp_NY))
relative_point = relativeneigh(shp_point)
weigh_relative = graph2nb(relative_point)
plot(st_geometry(shp_NY), main = "Relative neighbor graph")
plot(weigh_relative, shp_point, add = T, col = "red")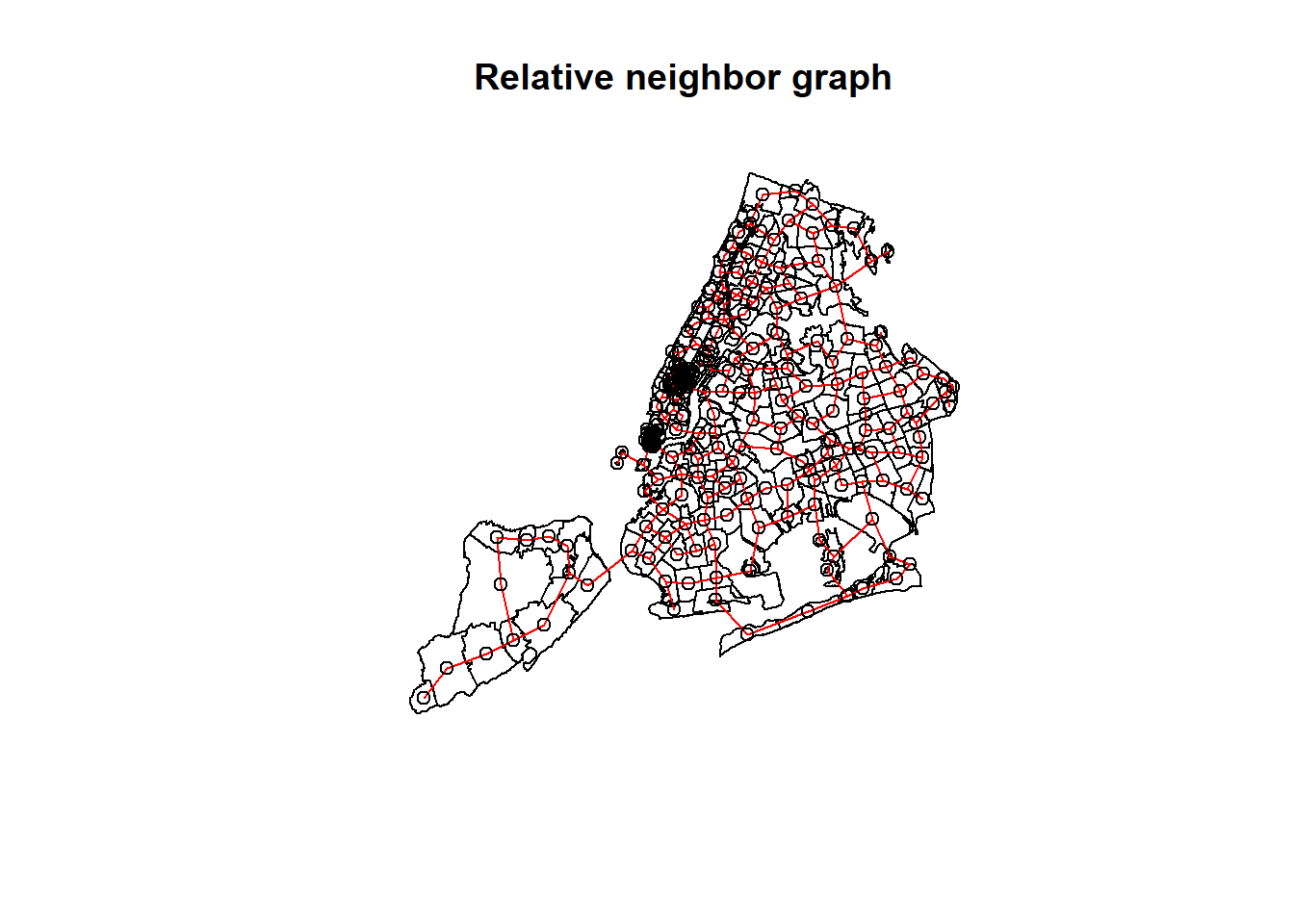
weight_NY =nb2listwdist(weigh_relative, shp_NY, type="idw", style="raw",
alpha = 1, dmax = NULL, longlat = NULL,
zero.policy=TRUE)
weight_NY_matrix = listw2mat(weight_NY)The figure above shows the adjacency relationships used in this study. It posits that areas connected by red lines may experience a spillover effect in dog bite incidents or dog keeping.
Considering the annual dog bite incident numbers for each zipcode in New York City from 2015 to 2021, the Moran scatter plot below preliminarily illustrates the spatial autocorrelation of these incidents. The horizontal axis represents the count of dog bite events, while the vertical axis depicts the spatially lagged values of this variable. Each point corresponds to a specific zipcode.
shp_NYall = shp_NYall |>
mutate(sc = as.vector(scale(shp_NYall$count)))
dat = moran.plot(shp_NYall$sc, listw = weight_NY)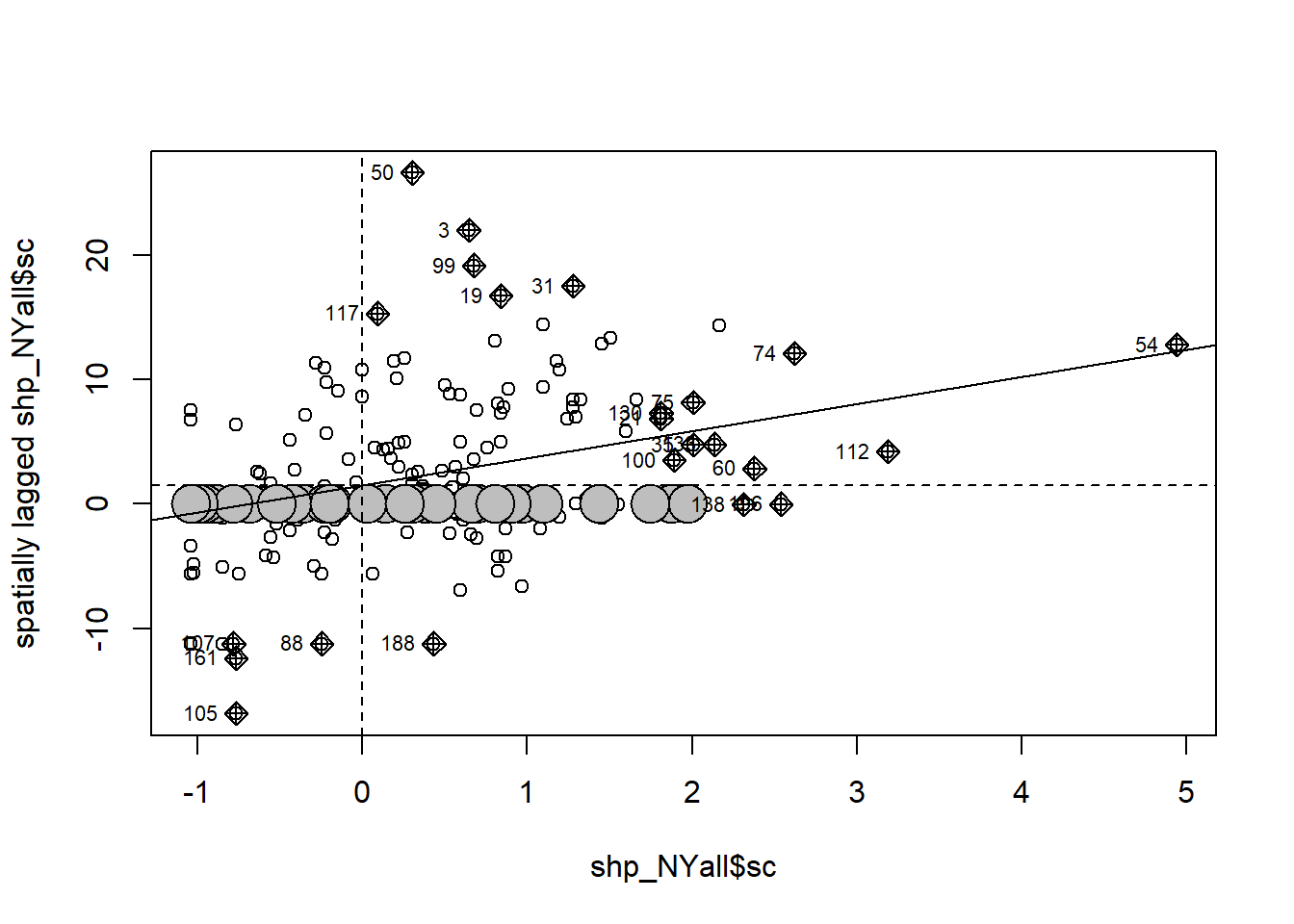
The correlation line, demonstrating a positive slope, indicates positive spatial autocorrelation, suggesting that similar values are clustered together spatially.
Additionally, the concentration of data points primarily in the first and third quadrants supports the presence of positive spatial autocorrelation, where spatially similar values are clustered. The presence of several outliers, especially in the second and fourth quadrants, may indicate that regions whose spatial distribution patterns deviate from those of their surrounding areas.
Analyzing dog bite incidents from 2015 to 2021, the observed global Moran’s Index is 0.35, which is greater than 0, and both the expected Moran’s I and the p-value are close to 0. Consequently, the distribution of dog bite incidents in New York City significantly exhibits positive spatial autocorrelation.
result <- moran.test(shp_NYall$count, listw = weight_NY)
summary_table <- data.frame(
Metric = c("Observed Moran's I", "Expected Moran's I", "Standard Deviation", "P-value"),
Value = c(result$estimate[[1]], result$estimate["Expectation"], sqrt(result$estimate["Variance"]), result$p.value)
)
kable(summary_table, digits = 3, caption = "Summary of Moran's I Test")| Metric | Value |
|---|---|
| Observed Moran’s I | 0.350 |
| Expected Moran’s I | -0.005 |
| Standard Deviation | 0.064 |
| P-value | 0.000 |
The annual global Moran’s I for the distribution of dog bite incidents are as follows, indicating that there is indeed a spatial correlation in New York City.
Moran_all = tapply(bite_counts$count, bite_counts$year, Moran.I, weight_NY_matrix)
moran_dat = data.frame()
for (i in names(Moran_all)){
moran_df = data.frame(year = i,
moran = Moran_all[[i]][[1]],
expected = Moran_all[[i]][[2]],
sd = Moran_all[[i]][[3]],
p.value = Moran_all[[i]][[4]] )
moran_dat = rbind(moran_dat, moran_df)
}
kable(
moran_dat,
caption = "Moran's I Results for Each Year",
col.names = c("Year", "Observed Moran's I", "Expected Moran's I", "sd", "P-value"),
digits = 3
)| Year | Observed Moran’s I | Expected Moran’s I | sd | P-value |
|---|---|---|---|---|
| 2015 | 0.141 | -0.004 | 0.061 | 0.018 |
| 2016 | 0.214 | -0.004 | 0.061 | 0.000 |
| 2017 | 0.221 | -0.004 | 0.061 | 0.000 |
| 2018 | 0.218 | -0.004 | 0.061 | 0.000 |
| 2019 | 0.164 | -0.004 | 0.061 | 0.006 |
| 2020 | 0.121 | -0.004 | 0.061 | 0.042 |
| 2021 | 0.175 | -0.004 | 0.061 | 0.004 |
Similarly, we can discover the correlation in the distribution of dog licenses across New York City. The global Moran’s Index of 0.29 suggests that similar values tend to cluster spatially, indicating that certain adjacent zip code areas may exhibit concentrations of dog ownership or areas where few dogs are kept.
license_counts_all = license |>
group_by(zip_code) |>
summarise(license_count = n())
shp_NYall_license = shp_NYall |>
left_join(license_counts_all,
by = c("ZIPCODE" = "zip_code")
) |>
mutate(license_count = ifelse(is.na(license_count), 0, license_count))
shp_NYall_license = shp_NYall_license |>
mutate(license_sc = as.vector(scale(shp_NYall_license$license_count)))
result <- moran.test(shp_NYall_license$license_count, listw = weight_NY)
summary_table <- data.frame(
Metric = c("Observed Moran's I", "Expected Moran's I", "Standard Deviation", "P-value"),
Value = c(result$estimate[[1]], result$estimate["Expectation"], sqrt(result$estimate["Variance"]), result$p.value)
)
kable(summary_table, digits = 3, caption = "Summary of Moran's I Test")| Metric | Value |
|---|---|
| Observed Moran’s I | 0.293 |
| Expected Moran’s I | -0.005 |
| Standard Deviation | 0.064 |
| P-value | 0.000 |
Local Moran’s I
To further explore specific areas exhibiting spatial clustering, the involvement of local Moran’s I is necessary. The formula for this index is as follows:
\[ I_i = \frac{{y_i - \bar{y}}}{{S^2}} \sum\limits_{j \ne i}^n w_{ij} (y_j - \bar{y}) \]
Where \(n\) represents the total number of spatial elements, \(S^2 = \frac{1}{n} \sum_{i=1}^n (y_i - \bar{y})^2\), \(y_i\) and \(y_j\) denote the attribute values of the \(i^{th}\) and \(j^{th}\) spatial elements, respectively, \(\bar y\) is the mean of the attribute values for all spatial elements, \({w_{ij}}\) is the spatial weight between elements \(i\) and \(j\). \(I_i\), the local Moran’s I of the \(i^{th}\) spatial elements, is not restricted in range. The specific implications of local Moran’s I are as shown in the following table.
data <- data.frame(
col1 = c("> 0", "< 0", "< 0", "> 0"),
col2 = c("> 0", "< 0", "> 0", "< 0"),
col3 = c("> 0", "> 0", "< 0", "< 0"),
col4 = c(
"The attribute of the i-th element is high, and the attribute of the surrounding element is also high.",
"The attribute of the i-th element is low, and the attribute of the surrounding element is also low.",
"The attribute of the i-th element is low, but the attribute of the surrounding element is high.",
"The attribute of the i-th element is high, but the attribute of the surrounding element is low."
)
)
colnames(data) <- c(
"${y_i} - \\bar{y}$",
"$\\sum\\limits_{j \\ne i}^n w_{ij}({y_j} - \\bar{y})$",
"${I_i}$",
"$Implication$"
)
kable(data, format = "html", escape = FALSE, caption = "Implications of Local Moran's I") |>
kable_styling(full_width = FALSE) |>
column_spec(3, width = "4cm") | \({y_i} - \bar{y}\) | \(\sum\limits_{j \ne i}^n w_{ij}({y_j} - \bar{y})\) | \({I_i}\) | \(Implication\) |
|---|---|---|---|
| > 0 | > 0 | > 0 | The attribute of the i-th element is high, and the attribute of the surrounding element is also high. |
| < 0 | < 0 | > 0 | The attribute of the i-th element is low, and the attribute of the surrounding element is also low. |
| < 0 | > 0 | < 0 | The attribute of the i-th element is low, but the attribute of the surrounding element is high. |
| > 0 | < 0 | < 0 | The attribute of the i-th element is high, but the attribute of the surrounding element is low. |
The local Moran’s I for both dog bite incidents and dog licenses in each zip code are displayed in the map below. Zip code areas highlighted in red exhibit significant high-high spatial clustering for dog bite incidents, while those outlined in yellow show significant high-high clustering for dog licenses. This aligns with the characteristics of the study area. It is generally believed that dog owners tend to walk their dogs near their homes. Therefore, dogs with a higher likelihood of causing harm are more likely to impact nearby zip codes, leading to clusters of high incidence areas for dog bites. Given this behavior, it is reasonable that there are no significant high-low or low-high clustering patterns for dog bite incidents in the study area. Moreover, if an area with dog bite incidents shows a significant low-low clustering, it simply indicates that this neighboring region has fewer dogs compared to others. As there is no significant low-low clustering of dog licenses in New York City, the absence of significant low-low clustering of dog bite incidents is also justified.
locaI = localmoran(shp_NYall$sc, weight_NY, alternative = "greater") |>
as.data.frame() |>
setNames(c("I", "Expected_I", "Variance", "Z_score", "P_value"))
shp_locaI <- cbind(shp_NY, locaI) |>
mutate(I = ifelse(is.na(I), 0, I)) |>
select(-ST_FIPS, -CTY_FIPS, -SHAPE_AREA, -SHAPE_LEN)
locaI_license = localmoran(shp_NYall_license$license_sc, weight_NY, alternative = "greater") |>
as.data.frame() |>
setNames(c("I", "Expected_I", "Variance", "Z_score", "P_value"))
shp_locaI_license <- cbind(shp_NY, locaI_license) |>
mutate(I = ifelse(is.na(I), 0, I)) |>
select(-ST_FIPS, -CTY_FIPS, -SHAPE_AREA, -SHAPE_LEN)
###############################################################################
tmap_mode("view")
map_locaI =
tm_shape(shp_locaI, name = "all zipcode") +
tm_polygons(col = "#f4f4f4") +
tm_shape(shp_locaI |> filter(I > 0 & Z_score > 0 & P_value < 0.05), name = "High-High") +
tm_polygons(
"I",
palette = c("#f4f4f4","red","yellow"),
title = "Local Moran's I",
breaks = c(0, 0.000001, 100, 1000),
labels = c("Non-Significant", "High-High (Dog Bite)", "High-High (License)")) +
tm_shape(shp_locaI_license |> filter(I > 0 & Z_score > 0 & P_value < 0.05), name = "High-High") +
tm_borders(lty = "solid", lwd = 2, col = "yellow") +
tm_layout(title = "Local Moran's I for Dog Bite and License", legend.show = TRUE)
map_locaIThe zip codes 10029, 10035, 11217, and 11237 on the map all exhibit significant high-high clustering for both dog bite incidents and licenses, with neighboring areas also showing trends of high concentrations of dog licenses. This indicates that a higher number of dogs in these areas is a non-negligible factor contributing to the increase in dog bite incidents. Additionally, there is a significant high-value clustering of dog bite incidents in the northern part of New York City, without a corresponding high concentration of dog ownership. Future research should focus on exploring other potential factors that may increase dog bite incidents in this area, such as management of parks that allow dogs, local dog ownership environments, and regulatory policies.